Implementation of ID3 Decision Tree Algorithm
**All code used have been uploaded to Github**
This task lets us implement a simple machine learning algorithm, such as ID3 decision tree algorithm or perceptron training algorithm or integration method. The task also includes a reflection report on our development, testing solutions and results. Here I am using an application of ID3 decision tree algorithm.

The general outline of this post is as follows:
-
Introduction to Decision Tree
-
What is ID3 Algorithm and how does it work?
-
Explain the role of entropy and information gain and how they work.
-
Experiment Design and Evaluation
-
Conclusion
Tools: Python & Goggle Colab
Introduction
Decision tree is a supervised learning model that can be applied to classification and regression problems. Decision tree model essentially summarizes a set of classified rules from a training dataset. It can be thought of as a set of if-else statements, or can also be a conditional probability distribution defined in a feature space. Through the rules obtained in the training set, the unknown data is predicted and classified.
A decision tree mainly consists of three parts: tree nodes, branches and leaves. Each tree node represents a problem or a decision and is also an attribute of the classification object. A branch represents a condition of division, and a leaf represents a result. Building a decision tree is a recursive process of selecting nodes in the tree, calculating the branches of the partition conditions, and finally reaching leaf nodes.
In this report, there will be a detailed introduction to the ID3 algorithm by using the PlayTennis dataset, including the use of entropy calculation and information gain calculation, data preparation, model building and result evaluation, etc. At the end of the report, the decision tree and ID3 algorithm will be summarized as a whole.
ID3 Algorithm
The ID3 (Iterative Dichotomiser 3) algorithm was first proposed by J. Ross Quinlan at the University of Sydney in 1975 as a classification prediction algorithm. The algorithm is based on information theory, and is measured by information entropy and information gain. By calculating the information gain of each attribute in the dataset, selecting the attribute with the highest information gain as the division criterion, and repeating this process, the recursive process is completed when no more divisions can be made or a single class can be applied to a branch.
The ID3 algorithm mainly includes the following steps:
1) Calculating the entropy of the dataset
2) For each attribute
I. Calculating the entropy of all attributes
II. Calculating the information gain of all attributes
3) Using the ID3 algorithm to build a decision tree and train the data
4) Making predictions
Entropy
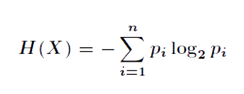
Information entropy is used to express the degree of uncertainty of a thing. If the uncertainty of the thing is higher, the information entropy of the thing is higher. Assuming a set S, if all members of S belong to the same class, then Entropy(S)=0. It also means that there is no impurity in this set. If the number of positive and negative samples of S is equal, in this case the value of entropy is the largest, then Entropy(S)=1. If the number of positive and negative samples of S is not equal, then Entropy(S) is between 0 and 1. In short, entropy characterizes the purity of the sample set. Entropy quantifies the uniformity present in the set of samples, and the purer, the lower the entropy.
If the value of a random variable X is X= {x1, x1, …, xn}, and the probability of each obtaining is {p1, p1, …, pn}, then the entropy formula of X is:
The screenshot below shows the code implementation of entropy calculation, as shown in Figure 1. First, the function for calculating entropy (Line 3-Line 4) is created. Line 8-10 calculates the proportion and probability of the target attribute class through the for loop, and finally returns it to entropy through return (Line 11).

Figure 1 # Entropy calculation function
Information Gain
Information gain is an crucial index for feature selection in decision tree classification. It is defined as how much impact a feature can have on the classification system. If the value of information gain is larger, it means that the feature is more important, and the attribute is higher in the decision tree.
The calculation of information gain is the difference between the information before and after the decision tree performs attribute selection and division. As shown in the following formula, where Entropy(S|T) represents the conditional entropy of the sample under the condition of the feature attribute T, then the information gain of the attribute feature T is finally obtained:
The code for the information gain function is as follows:
As shown in Figure 2, three main parameters are included in this function: df, split_attribute_name and target_attribute_name. The attribute that needs to be split is to select the attribute with the largest information gain for segmentation after calculating the information gain, and the target attribute is the predicted column in the data set. The code of (Line 4) is divided by gourpby, and (Line 6-9) is the formula for calculating the entropy of the target attribute. Finally, the current information gain value (Line 11-13) is obtained by subtracting the attribute entropy value from the entropy before the attribute selection division.


Figure 2 # Information gain of Attributes
Model Evaluation
Here the model will be evaluated on the PlayTennis dataset
Data Preparation
In the PlayTennis dataset, there are a total of 14 weather records with four attributes: outlook, temperature, humidity and wind. The learning objective is whether to go out to play (yes or no). That is, we know the values of the first four columns and predict the value of the last column by training on the dataset.
Experiment Design and Evaluation
Step 1: Calculate the information entropy of the target attribute (Amount of uncertainty in the dataset)
According to the function above (Refer to Figure 1 & 3), it can be calculated:
Total Entropy of PlayTennis Data Set: 0.9402859586706309
Step 2: Calculate the information gain of each attribute in the dataset: outlook, temperature, humidity and wind
Info-gain for Outlook is :0.2467498197744391
Info-gain for Humidity is: 0.15183550136234136
Info-gain for Wind is:0.04812703040826927
Info-gain for Temperature is:0.029222565658954647
By calculating the information gain of the above attributes, we can find the attribute with the largest information gain of outlook. At the same time, it is indicated that outlook is also the most important for play, so the root in the decision tree will be 'outlook'.
Step 3: Build a decision tree using the ID3 algorithm
In the construction of the ID3 algorithm decision tree (Refer to Figure 5 & 6), there are three main parameters, namely ‘df’, ‘target_attributes_name’ and ‘attribute_name’. The first is to use 'Counter' to calculate the class proportion of the target attribute in each attribute (Line3). Then, the feature returns with the most occurrences are then divided. If all categories are the same, it will remove this attribute and no further division is required (Line4-8). In the dataset partition, first it will get the default value (Line 10) for the next recursive call of this function. Then the information gain for each attribute is calculated and the highest information gain attribute is selected (line 11-line14). After that, choose the best attribute for splitting (line16). Line19-20 creates an empty tree and uses the attribute with the best information gain as the root node. Finally, this process will be repeated, and at each split, the algorithm will be called recursively to complete the creation of the tree (line 25-28).
After multiple traversal processing, a tree structure will eventually be obtained.
List of Attributes: [‘outlook, ‘temperatwre’, ‘humidity’, ‘wind’, ‘play’]
Predicting Attributes: [‘outlook’, ‘temperature’, ‘humidity’, ‘wind’]
Decision tree:
{‘outlook’: {‘overcast’: ‘yes’, ‘rainy’: {‘wind’, {‘strong’: ‘no’, ‘weak’, ‘yes’}}, 'sunny’: {‘humidity’:
{‘high’: ‘no’, ‘normal’: ‘Yes}}}}
This tree structure is also visualized, as shown in the following figure (Refer to figure 7):
Step 4: Decision Tree Accuracy
Finally, there is a calculation and validation of the classification accuracy (Refer to Figure 8 & 9). Through checking, it can be found that the predicted value is consistent with the target attribute, and the accuracy rate is 1. This is not difficult to understand, mainly because the predicted column itself is inferred from the original data

Figure 3 # The information entropy of attribute[‘play’]

Figure 4 # Information gain of each attributes

Figure 5 # ID3 Algorithm execution

Figure 6 # ID3 algorithm to construct decision tree
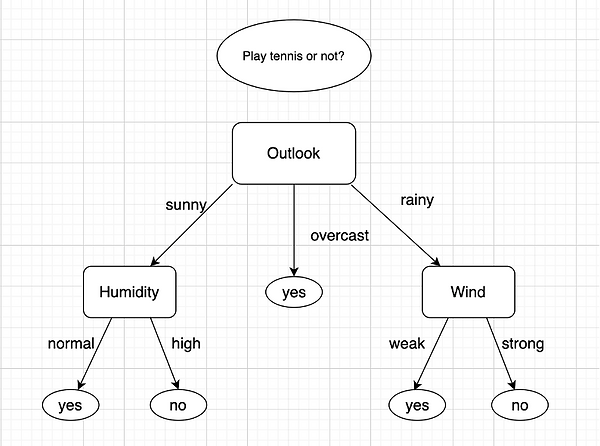
Figure 7 # Decision tree structure diagram


Figure 8 & 9 # Classification accuracy
Evaluation Results
As shown in the figure below, this dataset is split to further evaluate the prediction results. The first ten instances are used as the training set, and the last four are used as the test set. It can be found that when the data set is divided into two parts, the accuracy of the model becomes "75"%. In this case, there is a big reason that there is a certain error due to too few training set samples.

Figure 10 # Split the dataset and predict
Conclusion
Decision tree is a very common classification method. It is easy to understand and implement, and the decision tree model can be easily imagined and visualized. For decision trees, the complexity of the decision tree algorithm is small, and the ability to handle both numbers and categories of data produces feasible and well-executed results on large data sources in a relatively short period of time. However, the disadvantage of decision tree is that the decision tree model tends to produce an overly complex model, which will have poor generalization performance to the data. This is also called overfitting. In addition, for data with inconsistent number of different types of samples, the result of information gain in decision tree is biased to those features with more values.